merhaba,
öncelikle gönderdiğiniz resim tarafımıza ulaşmamıştır,
bir indikatör üzerine başka bir indikatör atabilirsiniz,
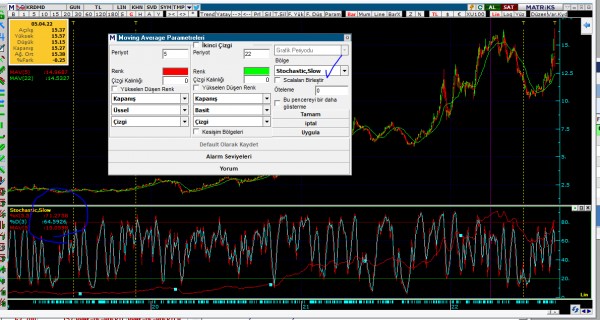
indikatörü atarken sadece bölge seçimi yapmanız gerekir,
ancak bazı indikatörler sabit bir değer arasında giderken(stochastik 20-80 arasında değer elır genellikle)
bazıları fiyata göre hareket ederler(hareketli ortalamalar fiyatı takip ederler 1000 tl bir senedin ortalaması 1000 değer alabilir)
dolayısıyla birbirlerini asla kesmezler
belirttiğini kesişim stoch ile mov(EMA) asla olmayabilir veya beklediğiniz sonuçları vermeyebilir,
resimde de görüleceği üzere stoch ve mov aynı yerlerdede gözükse değerleri birbirinden çok farklıdır,
bilgilerinize
iyi günler dileriz



